
When carrying, Kim first adds the carried number and then continues multiplying. Using this method, Kim will only get the correct answer for questions where there is no carrying necessary.
The strategies described below refer to some examples of Kim's written work. To see these examples, click here. Use your browser 'Back' button to return to this page.
Teaching strategies:
It is evident that Kim is able to efficiently and correctly solve single digit problems. Her errors are due to a mistake in the process she uses. This is often apparent when students are simply rote taught a set method, but lack the mathematical understanding behind the process. Kim needs to first realise that her method is faulty. This could be done through use of concrete materials or by checking with a calculator. Kim secondly needs to revise multiplying by a single digit with carrying. She needs to use the extended form (as shown below) until the procedure is familiar and the concepts (especially the distributive property) is well understood.
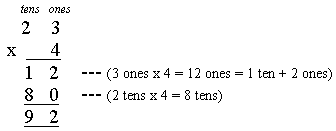
Back to Example completed diagnostic test for multiplication
Jane
When carrying, Jane retains the carried number from the units column and continues to add it at every stage. If two numbers have been carried into the tens column, she will add both.
The strategies described below refer to some examples of Jane's written work. To see these examples, click here. Use your browser 'Back' button to return to this page.
Teaching strategies:
Like Kim, Jane's errors are due to an error in the process rather than in computation. Jane needs to first realise that her method is faulty and then revise the correct method. Jane errors demonstrate that when completing the question, she is simply following a number of recalled steps rather than understanding the mathematical concept. Breaking the algorithm into a series of stages will help Jane master this process.
Back to Example completed diagnostic test for multiplication
Jolly
Jolly's method treats both numbers in the multiplier as units and completes the question in one line. He has used the process for multiplication by single digit numbers to invent a process for multiplying by two or more digits. When multiplying by two digit numbers, Jolly will first multiply the two unit values together and then his second step is to multiply the two tens values together. Jolly will only answer single digit multiplication problems correctly.
The strategies described below refer to some examples of Jolly's written work. To see these examples, click here. Use your browser 'Back' button to return to this page.
Teaching strategies:
From looking at Jolly's work it seems apparent that he is not familiar with the process of long multiplication by two or more digits. None of his answers show any evidence of experience with this process. Jolly is competent with multiplication by one digit (the first stage of multiplication) and is now ready to be introduced to multiplication by multiples of ten and then to multiplication by numbers of two or more digits. Work with concrete materials, checking of answers with calculators and breaking down the process are all strategies that will need to be included when teaching Jolly the next two stages.
However, it may also be the case that Jolly has been introduced to these stages but continues to revert to his invented form. It is indeed true that some students will never really master multiplication of two or more digit numbers. If this is the case with Jolly, he needs to be alerted to the fact that his method gives nonsense answers (such as in problem 4) and assisted to develop a strategy of checking his answers.
Back to Example completed diagnostic test for multiplication
Sid
When completing the question Sid treats both numbers as units, forgetting to place a zero in the units column before multiplying by the tens. Sid will only answer single digit multiplication problems correctly.
The strategies
described below refer to some examples of Sid's written work. To see these
examples, click here. Use
your browser 'Back' button to return to this page.
Teaching strategies:
Sid's error is common with many children when moving from single digit to two digit multiplication. Sid treats both numbers in the multiplier as units. Sid needs to revise the concept behind each step of the multiplication process. He needs to realise that a 3 in the tens column is not a three but rather 30. More work with multiplication by multiples of ten and writing out the sum for each step as followed will assist Sid at this stage of his development.
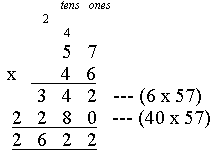
Solving problems in small groups orally with the teacher as scribe is also an important step in Sid's development. Being able to orally explain the process will assist students to consolidate knowledge.
Back to Example completed diagnostic test for multiplication
Tom
Tom's Error: a x 0 = a
Unlike the other examples where the errors where due to process, Tom's errors are due to a mistake in computation. Tom has a misunderstanding about the properties of zero. Tom will only answer questions correctly if there is no zero in either number. His answer to problem four is correct.
The strategies described below refer to some examples of Tom's written work. To see these examples, click here. Use your browser 'Back' button to return to this page.
Teaching strategies:
Tom needs to be reminded about the properties of zero. Zero is a difficult concept to demonstrate with concrete materials, so discussing worded examples may help Tom understand his mistake better. An example may include: I have five bags with no lollies in each, how many lollies do I have altogether?
Tom may also be typical of students who work too quickly. Although competent with the processes and most of the computation, he makes silly mistakes as he is careless. Students like this can benefit from being made to check their work before submission and rewriting and solving incorrect problems again.
Back to
Example completed diagnostic test for
multiplication
![]()